1 引言
导航是智能车领域中基本问题,其任务是利用传感器获得的量测信息,对智能车当前位置进行精确的估计。智能车正常行驶中,动态模型通常都是在笛卡尔坐标系下建立的,而全球定位系统(Global Positioning System,GPS)量测值都是以极坐标形式表示,因此,智能车位置估计也就变为一个非线性估计问题[1-3]。
当模型中的非线性因素不可忽略时,通常采用非线性滤波进行状态估计。应用较广泛的方法是扩展卡尔曼滤波器(Extended Kalman filer,EKF)[4-5],这种方法存在线性化误差大、雅可比矩阵难于计算等缺陷,滤波不稳定,甚至发散[6-7]。S.J.Juliear和J.K.Uhmann在1997提出基于无迹(Unscented,UT)变换的无迹卡尔曼滤波(UnscentedKalman Filter,UKF),其均值和协方差的估计比EKF方法要精确[7]。
UKF虽然克服了EKF存在的一系列问题,但系统噪声相关信息的不确定性以及状态模型扰动等都会影响UKF的滤波精度。鉴于此,本文提出了一种带衰减因子的自适应无迹卡尔曼滤波算法(IMM—AFUKF),该算法基于交互式多模型结构(Interacting multiple mode,IMM) [3],克服了模型不确定性因素的影响,并引入衰减因子及自适应渐消因子[3]来修正预测误差协方差,调整滤波增益,减弱旧数据对滤波的影响,从而消除滤波的发散现象。最终得到具有更高精度、更强抗扰动能力的滤波器,以满足无人驾驶智能车控制系统的需求。
2 智能车导航系统控制原理
2.1无人驾驶智能车控制系统
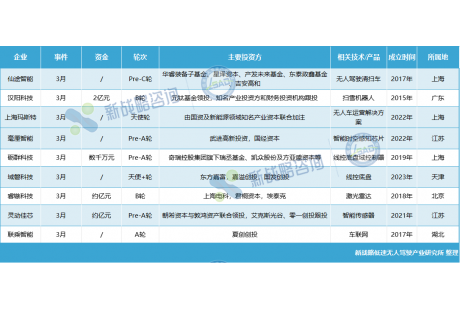
本文以北京工业大学无人驾驶智能车BJUT—IV为对象,研究其位置估计问题。BJUT—IV控制系统包含三大模块:环境感知模块,决策模块,底层控制模块,如图1所示,其中环境感知模块主要包括车外环境感知模块、导航定位模块、车体信息模块。其中导航定位模块提供车辆在全局地图中的位置和速度,用于全局路径规划、路径跟踪,是否能提供快速、准确、可靠的导航信息直接决定上位机的决策的正确性,并最终影响底层控制的效果。
2.2导航系统车体位置模型
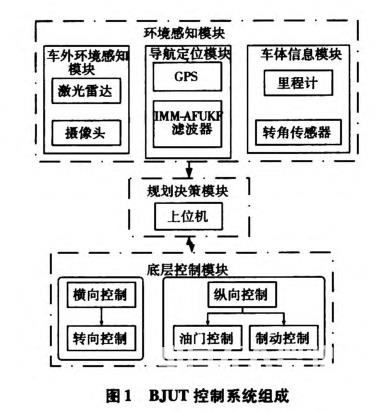
BJUT—IV采用GPS作为导航系统,GPS输出坐标为ECEF坐标系统下的经度、纬度、高度,并不适合于平面运动的车辆导航。本文采用通用横轴墨卡托坐标系(Universal Transverse Mercator,UTM)将经纬度转化到平面坐标系,如图2所示UTM坐标系统原理。在实际应用中,UTM坐标的转换公式较为复杂,且在系统中有实时性的要求下很难达到,因此本文采用经过简化处理的一组UTM坐标转换公式[8-9],篇幅限制不再赘述。将坐标原点o定于北纬39.8719,东经116.4789,车体位置相对坐标原点关系如图3所示。

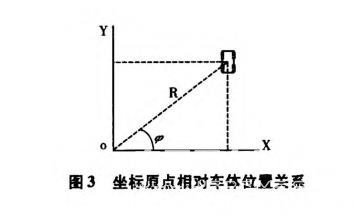
在直角坐标系下,车辆所处位置的方位角、斜距之间关系为

BJUT—IV的主要运动方式为匀加速行驶、匀速行驶、匀速水平转弯,本文在不影响实际模型精度的情况下将匀速水平转弯运动状态近似为匀速行驶状态。BJuT—IV行驶轨迹水平高差均值为41.6/m,无明显高差,因此车辆纵向运动轨迹问题本文不加考虑。
为验证提出的带衰减因子的自适应滤波算法IMM-AFUKF的性能,文章第四部分将其与基于IMM模型的UKF滤波算法、基于匀加速运动模型(CA)的EKF滤波算法进行了仿真及实验的对比和分析。
2.3导航系统运动控制模型
根据智能车的运动状态与典型模型匹配程度及其复杂性,本文选择两个典型的二维智能车运动控制模型建立IMM模型组,分别为匀速运动控制模型(Constant Velocity,CV)、匀加速运动控制模型(Constant Acceleration,CA)[10-11]。
智能车运动学模型可表示为

匀加速模型(Constant Acceleration,CA)取状态变量X
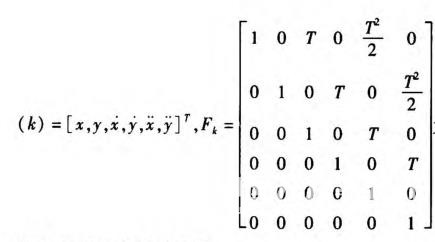
为状态转移阵,其它参数设置同上。
2.4滤波器量测模型
量测方程可由下式给出

2.5智能车导航系统技术难点
导航定位模块中GPS提供的速度、位置、航向等导航定位信息本身带有噪声,且由于环境因素会产生较大误差,需通过滤波器滤波后发,发送至决策计算机进行决策并完成车体控制。
因此,研究具有更高性能的滤波器意在为车辆控制系统提供更快速、准确而稳定的地理位置及速度信息。进一步讲,滤波器的性能直接决定了导航定位系统的性能,并最终影响车体控制。所以,对于滤波器的优化在导航定位系统乃至车辆控制系统中具有十分重要的意义。
现阶段导航系统中,针对滤波器的研究仍然存在以下几个难点问题:①实际路况中,存在大量非线性因素:智能车导航系统中滤波器普遍采用的扩展卡尔曼算法(EKF) [8],该算法虽能实现非线性滤波,但是滤波精度已无法满足智能车导航的需求;②实际车况下,车辆运动状态多变:目前采用无迹卡尔曼滤波(UKF)或UKF的优化算法[7],在精度上较传统的EKF有较大提高,但对于所提出的滤波算法的验证局限于理想化的仿真模型,依旧无法与真正智能车行驶状态相匹配;③由于真实路况下噪声干扰,会造成滤波效果降低甚至发散:鉴于车辆行驶状态的多变性,有学者提出采用交互式多模型(IMM)来逼近车辆真实状态[15],取得较好滤波效果,但算法不具有自适应性,且历史数据对滤波影响较大。因此,如何找到一种高精度的,可靠的,具有自适应性且能与无人驾驶智能车导航系统相匹配的滤波算法,仍然是现阶段工作的技术难点。
3 多模型无迹卡尔曼滤波算法
3.1算法原理
模型的匹配性不佳和噪声统计特性的不准确经常导致UKF滤波性能降低[12-13],为了解决这一问题,本文引用自适应UKF滤波(Adaptive UKF,AUKF),该方法通过自适应渐消因子来平衡状态方程、预测信息与观测信息的权重,能实时地对模型误差和噪声统计特性进行估计并修正,较好地抑制模型误差对导航解的影响,从而提高UKF的估计精度[14]。同时,加入衰减因子(Fading factor)[15-16],加大当前观测量的作用,减小历史观测值的影响,达到抑制滤波发散目的。AFUKF有效克服了噪声及与模型不匹配的不足问题,但对模型描述准确性仍要求较高,引入交互式多模型算法(IMM)可较好解决此问题。IMM包含多个滤波器、模型概率估计、交互作用器、状态估计混合器,基本原理为:通过建立不同的模型来描述系统可能的运动模态,模型间的切换由基于马尔可夫链的转换概率控制,对每个模型采用独立的AFUKF,以模型转移概率加权后的交互值作为滤波迭代输入。通过输出残差不断更新模型概率,对多个滤波器进行融合,使其尽可能地接近那个最能反映实际系统行为方式的模型滤波输出。AFUKF是UKF的优化,作为IMM结构中的并行滤波器,以下称为IMM-AFUKF算法,结构示意图4所示。
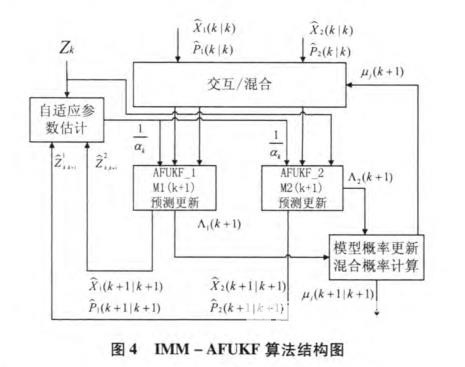
3.2算法流程
IMM—AFUKF算法具体步骤如下所示:
步骤1:计算混合概率系统非线性随机的状态空间模型为

步骤2:交互/混合

步骤3:模型滤波



4 仿真分析及实验
4.1仿真及实验分析
实验室的智能车辆实验平台安装应用载波相位技术的差分GPS(DGPS),设备组为FlexPak-G2系列GPS接收处理机和GPS-702-GG接收天线及PDL4535数传电台。设备实物如图5所示,GPS-702-GG接收天线关键参数如表1所示,FlexPak-G2系列GPS接收处理机关键参数如表2所示。



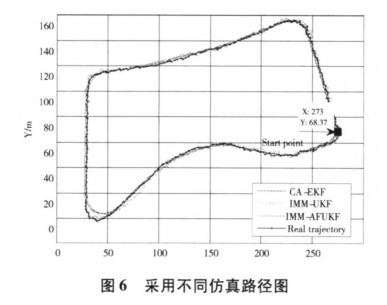
从仿真路径图中可看出,IMM-AFUKF与真实路径最接近,误差最小,CA-EKF,IMM-UKF均在弯道处理方面较为逊色。
同时,实验的采用均方根误差(Root mean square error,RMSE)定量分析并衡量算法优越性[1-3],其定义为
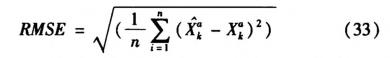
其中,n=500。RMSE越小,说明所采用的算法与真实值的误差越小;运行时间越短,说明算法的计算量越小,在实际应用中数据输出速度越快。图7~12为采用三种滤波方法位置、速度、加速度均方根误差曲线比较,表3为三种滤波算法均值和均方根误差统计数据。
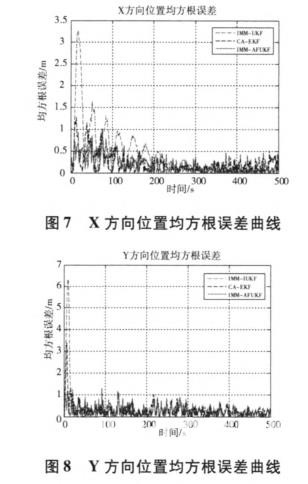
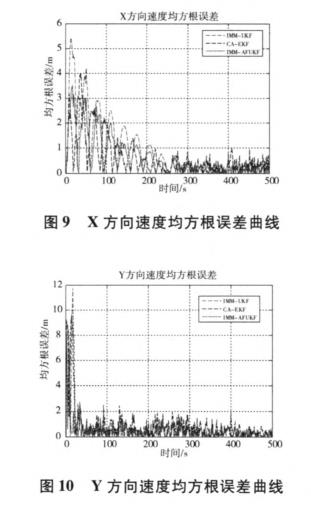
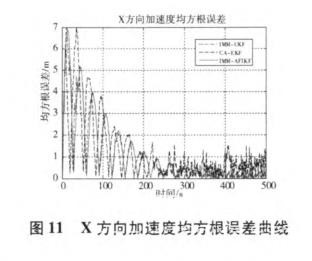
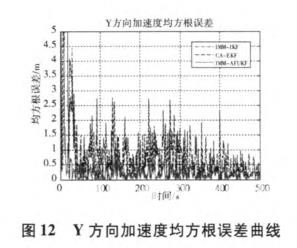
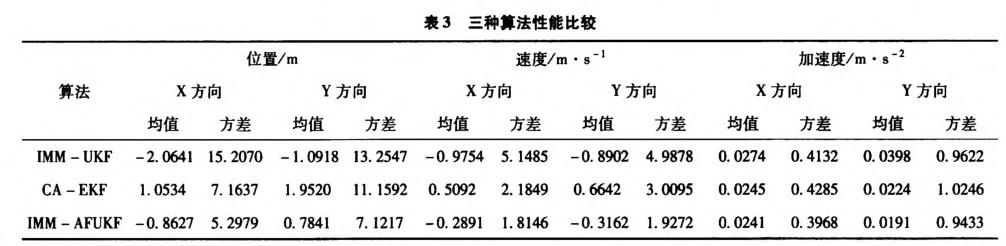
从仿真结果及性能统计值比较可以看出,在仿真的初始时刻,滤波器都有较大的初始偏差,这是由于初始估值造成的。随着滤波的进行,IMM-AFUKF算法能很快地收敛到真值位置附近,并保持较高的滤波精度。IMM-AFUKF算法较IMM-UKF、CA-EKF算法提高了解算精度及收敛速度,状态估计也更接近于真实状态,且增强了数值稳定性,其中IMM-AFMUKF算法的位置和速度的均方根误差明显小于标准IMM—UKF算法。究其原因,主要在于IMM-AFUKF算法引入了衰减因子,加大了对新测量值的利用权重,减少了对陈旧测量值和初始估值的依赖,同时增加自适应渐消因子,能够较好的抑制初始值偏差和模型异常扰动误差对导航解的影响,使算法具有一定的自适应能力。因此,IMM-AFUKF算法有效的控制了初始值偏差、模型异常扰动误差、以及未知噪声对滤波解的影响。
4.2实车实验
本文以北京工业大学无人驾驶智能车BJuT-IV为实验对象如图13所示,研究其行驶轨迹的跟踪问题。
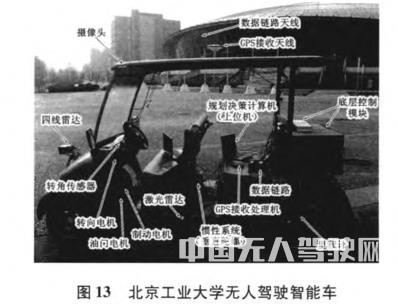
BJUT-IV由高尔夫球电动车经过对电控系统的改装而成。BJUT-IV采用GPS作为导航系统,并用UTM将经纬度转化到平面坐标系,重新定义坐标原点O于北纬39.8719,东经116.4789即图14中N8点为原点。BJUT-IV控制系统以Microsoft VS2008为软件开发平台,编写了导航与定位系统软件,利用此软件平台进行实验验证,用以检验IMM-AFUKF算法在智能车导航系统中的可靠性。实验分别采用KF(绿色轨迹)、IMM-UKF(黄色轨迹)、CA-EKF(蓝色轨迹)、IMM-AFUKF(红色轨迹)对实际道路采样点进行滤波估计(橙色轨迹代表真实道路)。取智能车的运动参数(位置、速度、加速度)作为系统的状态变量,采用东北天坐标系。
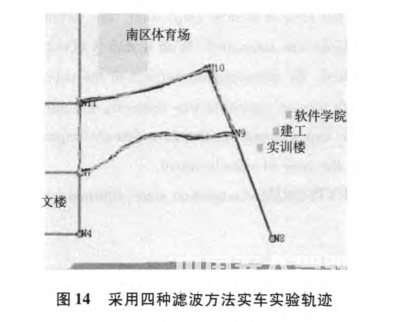
实验车辆沿道路车道线线行驶,根据实际情况做变速及匀速运动。实车实验结果表明,IMM-AFUKF算法较其它算法更准确、稳定;且在车辆转弯时性能更加突出,如图14中N10点和N9点弯道放大图所示,红色轨迹(IMM-AFUKF)几乎与橙色轨迹(实际道路)重合,黄色轨迹(IMM-UKF)与绿色轨迹(KF)均与实际行驶轨迹有较大偏差且有较大滞后性。所提出算法更贴切的反应车辆实际行驶轨迹,该实验结论与仿真结果一致,再次验证所提出算法优越性。
5结束语
在北京工业无人驾驶智能车BJUT-IV导航系统中,UKF处理非线性问题较EKF性能优越,然而,UKF算法对模型匹配度要求较高、受系统噪声影响较大,且对初始值较敏感,为此,本文在UKF中引入衰减因子及自适应渐消因子,并结合IMM滤波结构,提出了一种针对BJUT-IV导航系统的滤波算法IMM-AFUKF。理论分析、仿真、实车实验结果均表明,IMM-AFUKF算法的滤波精度、稳定性、收敛速度都明显优于标准IMM-UKF及EKF算法,具有较高实用价值。
该算法改善了导航系统精度,为上位机的控制决策提供良好的导航信息数据,将无人驾驶智能车控制系统整体性能进行了提升。为进一步改进IMM-AFUKF对初始值过于敏感等情况,需要在鲁棒性方面做进一步的探讨;并需克服模型转换时滤波精度降低的问题,以上两点将作为后续工作重点。
参考文献:
[1]杨柳.改进卡尔曼滤波的目标跟踪研究[J]·计算机仿真,[J] 2010—9:351—355.
[2]付梦印,邓志红,张继伟.Kalman滤波理论及其在导航系统中的应用[M].北京:科学出版社,2003.
[3]秦永儿,张洪城,汪叔华.卡尔曼滤波与组合导航原理[M].西安:西北土业大学出版社,1998.
[4]Yang Yuanxi,Gao Weiguang.A new learning statimic for adaptive filter based on predicted residuals[J].Progress in Natural SCience,2006—8:833—837.
[5]Cui Xianqiang and Yang Yuanxi.Adaptively robust filtering with classified adaptive factors[J].Progress in Natural Science,2006—8:846—851.
[6]Gao Sheshenga,Gao Yia,Zhong Yongminb,Wei Wenhuia.Random Weighting Estimation Method for Dynamic Navigation Positioning[J].Chinese Journal of Aeronautics,2011—3:318—323.
[7] 黄铫,张天骐,高清山,李越雷.一种提高无迹卡尔曼滤波精确度的方法[J].计算机仿真,2010,03:348—352.
[8] 王凡.智能车辆中基于GPS和陀螺仪的导航与定位[D].北京工业大学。2013.
[9] 王凡.智能车辆中基于GPS和陀螺仪的导航与定位[D].北京工业大学。2013.
[10] 潘泉,刘刚.联合交互式多模型概率数据关联算法[J].航空学报,999,(3):234—238.
[11]You Lilan,bu Dajie,Huang Jian,Liu Xue,Zhou Kechang.The Mathematic Models of the Kalman Filtering for Across—Fault Measurement[J].Earthquake Research in China,1994—3:92—103.
[12] 范韬,茅旭初.基于非线性滤波算法的高动态GPS定位模型[J].计算机仿真,2011—10:66—69.
[13] Liu Ye,Yu Anxi,Zhu Jubo,Liang Diannong.Unscented Kalman filtering in the additive noise case[J].Science China(Teehnological Sciences),2010-4:929—941.
[14] Hu Hmdong and Huang Xianlin.SINS/CNS/GPS integrated navisanon algorithm based on UKF[J].Journal of Systems Engineering andElectronics.2010一1:102—109.
[15] 陆可,肖建.IMM算法实现非线性状态估计的研究与仿真[J].计算机仿真,2008—5:77—80,104.
[16]Yang Yuanxi,Gao Weiguang.An optimal adaptive Kalman filter[J].Journal of Geodesy,2006,80(4):177 183.
[17]夏启军,孙优贤,周春晖.渐消卡尔曼滤波器的最佳自适应算法及其应用[J].自动化学报,1990—3:210—216.