0 引 言
无人驾驶汽车是未来智能交通的重要组成部分,其中车辆线控转向系统的控制是关键技术之一[1,2]。由于转向系统本身具有一定的非线性,并且在工作过程中存在负载变化大,易受外界干扰等特点,目前常用的PID控制[3]、滑模控制[4]等方法很难得到理想的控制效果.针对上述问题,采用自抗扰控制实现无人驾驶车转向系统的控制.自抗扰控制是由中科院系统科学研究所韩京清研究员提出的一种鲁棒非线性控制方法,该控制通过扩张的扰动观测器实时估计并补偿系统运行时受到的各种“外扰”和“内扰”的总和作用,并结合特殊的非线性反馈结构实现良好的控制品质,具有超调小、响应快、精度高、抗干扰能力强、算法简单等特点,并且适于数字化实现[5]。
1 无人驾驶车线控转向系统介绍
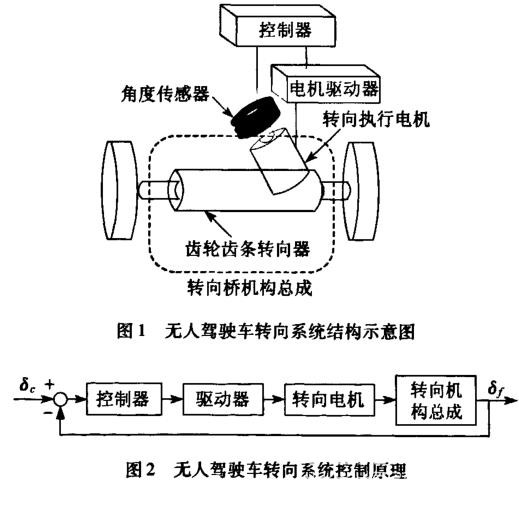
无人驾驶车转向系统的作用是根据路径规划指令,控制前轮的转动,使车辆沿规划的路径行驶.系统组成如图1所示。系统工作过程中,转向控制器根据路径规划指令,生成前轮转角命令信号。该信号将与角度传感器或齿条位移传感器反馈的实际前轮转角信号进行比较,利用两者的差值,通过一定的控制算法生成转向电机指令信号(电压或电流信号),指令信号再通过电机驱动器驱动转向电机转向,从而实现车辆方向的改变,整个系统的控制原理如图2所示。
2 转向系统动力学分析

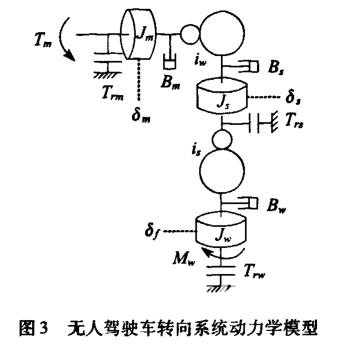
根据上述转向系统动力学模型,通过进一步向转向小齿轮的等效化简,得到转向系统的动力学方程如下:
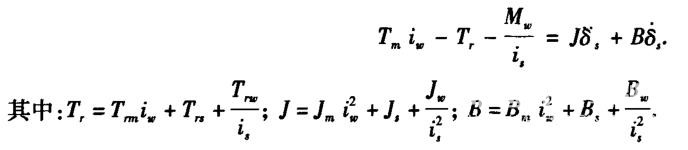
考虑到运用电机驱动器来对转向电机进行电流闭环控制,其控制带宽可达500 Hz,而转向系统的工作带宽小于10 Hz,因此这里不再考虑转向电机电磁特性对电机输出转矩的影响,将电机驱动器电压输入到电机电磁力矩输出简化为比例环节,即:

根据式(1)、(2)、(3),并将摩擦阻力矩Tr与Mw气假设为线性特性,可得整个转向系统传递函数如下:
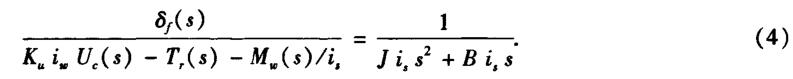
3 二阶自抗扰控制器的设计[6-8]
由上一节推导的转向系统传递函数可知,该系统的已知部分是—个二阶系统.根据自抗扰控制器的选择原则,控制对象的最小阶数决定自抗扰控制器的阶数,故这里选择二阶自抗扰控制器作为系统的控制器二阶自抗扰控制器由3个部分组成,即跟踪微分器、扩张状态观测器和非线性组合,其结构如图4所示。
图4中,V0为控制目标,V1是V0的跟踪信号,V2是V0的微分信号;Z1是控制对象输出y的估计信号,Z2是y微分的估计信号,Z3则是对系统状态和模型不确定性以及外部扰动的总体估计;e1、e2是误差及其微分,u为控制量,b0是对反馈放大系数的估计。
控制器各部分的离散表达式
(1)跟踪微分器
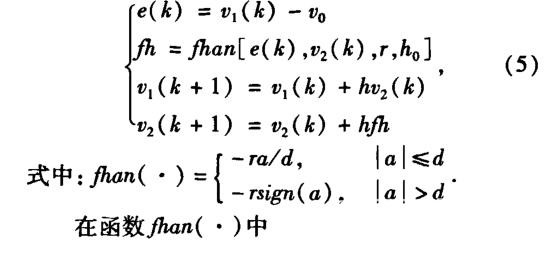
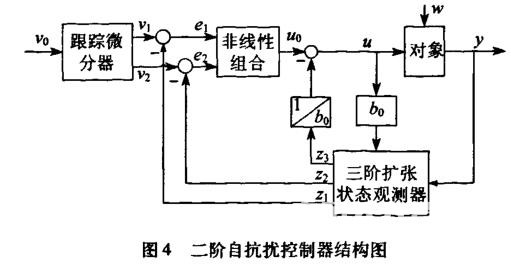
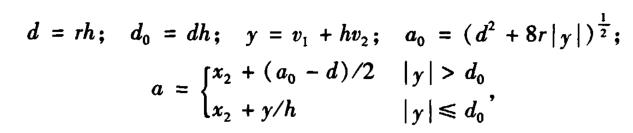
其中:h0为滤波因子;r为速度因子;h为积分步长。
跟踪微分器是一个非线性动态环节,它能够快速无超调地跟踪输入信号并给出较好的输入信号的微分。同时,通过对滤波因子h0和速度因子r的调节,可以使得控制目标的给出符合系统实际响应特性,从而有效地避免经典调节理论中因设定值的突变而造成控制量的剧烈变化以及输出量的超调,获得更为理想的控制特性。
(2)扩张状态观测器
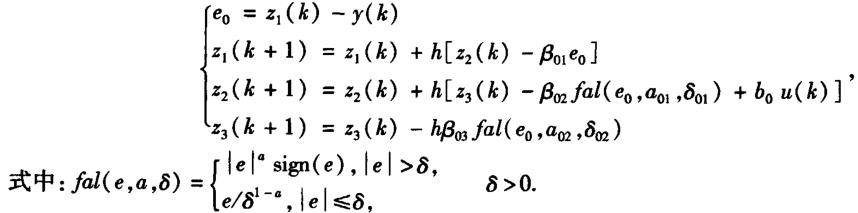
扩张状态观察器是自抗扰控制器的核心部分,它采用非线性状态观测器对系统的状态进行观测,其中的扩张的状态量是对系统状态和模型的不确定性等内扰以及外部扰动的反映.在控制量中,通过对扩张的状态量进行补偿,可将原来的控制系统转化为线性的积分串联型控制系统,大大增强了该控制器对系统的适应性.
(3)非线性组合
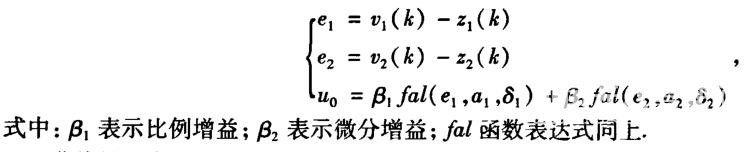
非线性组合实质是一种非线性状态误差反馈控制律,它将经典PID当中的线性加权转换成反馈效率更高的非线性组合,得到非线性PD控制器,以此提高系统的控制品质。
4 仿真研究
4.1整车模型介绍
为了更好地模拟轮胎回正力在不同工况下对转向系统的影响,本研究中的整车模型采用非线性七自由度车辆动力学模型[9],如图5所示.这里的七自由度是指汽车纵向速度、侧向速度与横摆角速度3个整车运动自由度和4个车轮的回转运动自由度。

其表达式如式(8)所示。


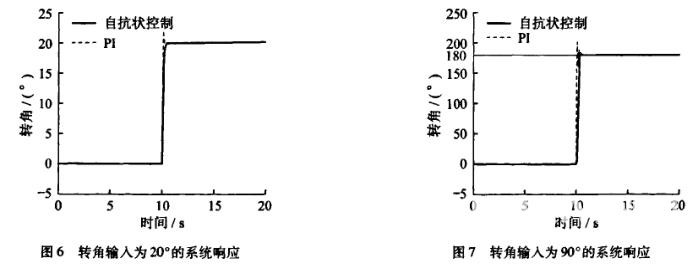
仿真研究首先检验了自抗扰控制器的控制能力,在车速为10 km/h的工况下,给车辆以阶跃转角信号200和180。(相当于前轮转角1.25度和11.25度),考察转向系统的输出响应,并与常用的PI控制器进行了对比,结果如图6,7所示.从图中可以看出:①自抗扰控制可以有效地实现对系统的控制;②由于设计了考虑系统自身响应能力的过渡过程,因而其控制效果好于PI控制,没有出现PI控制的超调现象;③对不同的转角输入自抗扰控制的适应性好,没有出现PI控制中由于控制目标的变化而出现动态过程变差的现象.如图7中所示,PI控制在转角输入为180度时动态过程振荡加剧,而自抗扰控制的动态过程和转角输入为20度时几乎是一样的。
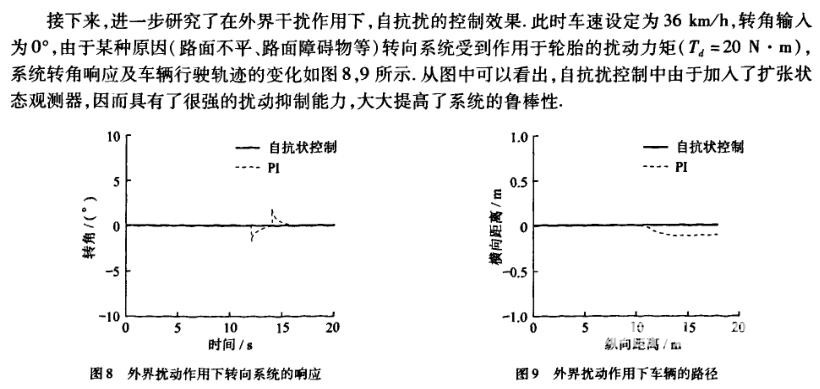
5 结论
针对无人驾驶车转向系统的特点,在分析转向系统动力学特性的基础上,设计了二阶自抗扰控制器来控制转向系统的转角.采用七自由度非线性车辆模型,在Madab/Smulink环境下进行了仿真研究。研究结果表明:
(1)自抗扰控制器可用于无人驾驶车转向系统的控制,具有较高的控制精度和很宽的控制范围;
(2)自抗扰控制器具有很强的扰动抑制能力,可有效提高系统的鲁棒性;
(3)使用自抗扰控制器无须获得控制对象的精确模型,简化了控制器的设计,提高了控制器的实际使用价值。仿真过程中,也发现了自抗扰控制器的一些问题:①控制参数较多,调节比较困难;②控制器的输出有一定的抖动.如何有效地解决上述问题,使自抗扰控制器能用于转向系统实际控制,将是下一步研究的重点。
参考文献:
[1] HOP,ST J,BARBERAA.Trajectory generation for an on.road autonomous vehicle[J].Proceedings of the SPIE。UnmannedSystens Technology VⅢ,2006,6230:62302J.
[2] 秦贵和,葛安林,雷雨龙.智能交通系统及其车辆自动控制技术[J].汽车工程,2001,23(2):92—96.
[3] BOLOGNAMI S,TOMASINI M,ZIGLIOTrO M.Control design of a steer—by—wire system with high performance PM motor drives[J].IEEE,2005,5:1839—1844.
[4] JANG S H,PARK T J,HAN C S.A control of vehicle using Steer-by·Wire system with Hardware·in-the-Loop—Simulation system[J].Proceedings of the 2003 IEEE/ASME,2003,3:389—394.
[5] 阮久宏,李贻斌,荣学文.高速移动平台横向运动自抗扰控制[J].山东工业大学学报(工学版),2008,38(4):5—10.
[6] 韩京清.从PID技术到“自抗扰控制”技术[J].控制工程,2002,9(3):13—18.
[7] 韩京清.扩张状态观测器参数与菲波纳奇数列[J].控制工程,2008,15(S1):1—3.
[8] 要晓梅,王庆林,刘文丽,等.一般工业对象的二阶自抗扰控制[J].控制工程,2008,9(5):59—62.
[9] 赵治国,余卓平,孙泽昌.车辆主动前轮转向H*鲁棒控制系统研究[J].汽车工程,2005,27(4):443—451.
[10] PACEJKA H B.Tm and Vehicle Dy,lamies[M].2nd ed.Burlington:Butterworth-Heinemann publications,2006.